Como calcular RPM de polias e engrenagens

Estava aqui fazendo um projeto em CAD, quando de repente comecei a calcular a força necessária para um determinado comportamento mecânico. Por sorte eu ainda estava no começo do projeto e não doeu tanto ter que abortar a operação. Mas durante os cálculos de engrenagem e cremalheira, acabei tendo alguns lapsos de memória, então resolvi escrever artigos chatos... digo, técnicos pra poder ter minhas próprias referências, porque não tenho muita paciência de ficar pesquisando no Google quando quero algo muito específico. A bola da vez é como calcular RPM.

Mudanças de velocidade

No caso de projetos DIY, as coisas são mais fáceis, porque temos facilidade de controlar a velocidade de motores DC simples, motores de passo e servo motores. Mas nem sempre temos o controle desejado. Normalmente a velocidade de motores é fixa e para variar as rotações, utiliza-se um conjunto de transmissão. Dependendo do conjunto de engrenagens ou polias, podemos ter mais ou menos velocidade no eixo final.

Transmissão idêntica

Conjuntos de engrenagens ou polias idênticas transmitem a mesma velocidade. Isso pode ser necessário quando o motor está longe do eixo final, mas temos o controle do motor, só nos interessa transmitir a frequência para o eixo.

Transmissão com redução de velocidade

É simples entender. Vamos pensar em 2 polias; uma de 5cm e uma de 10cm. A proporção é 1:2. Isso significa que a engrenagem menor tem que dar 2 voltas para que a grande complete uma volta. Logo, a engrenagem maior é mais lenta quando a engrenagem motora é a menor.

Transmissão com aumento de velocidade

Utilizando o mesmo exemplo, agora invertendo a engrenagem motora. A maior dará 1 volta e com isso a engrenagem menor rodará 2 vezes, logo, o resultado é o dobro da velocidade do eixo motor. Considerando isso, basta agora proporcionar as respectivas frequências.

Relação matemática para o cálculo

Uma relação para expressar esse fenômeno é representada como:

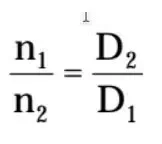
Nessa expressão, n1 e n2 são as RPM das polias motora e movida, respectivamente. Já D2 e D1 são os diâmetros das polias movida e motora. Lembre-se que devemos considerar o diâmetro primitivo sempre, seja polia ou engrenagem, pois trata-se do diâmetro de contato do conjunto mecânico. Quando lidamos com engrenagens, calculamos o RPM pelo número de dentes. Quando as engrenagens tem contato direto entre si, o passo é sempre igual para ambas (lembrando que o passo é a distância de 1 dente somando a 1 espaço). Considerando que o passo das engrenagens é o mesmo, a variação do número de dentes  fará com que as engrenagens tenham tamanho diferente, por isso a lógica descrita mais acima continua valendo.

A fórmula muda apenas de D (diâmetro) para Z (número de dentes).

Como calcular RPM de polias

Vamos utilizar valores bem pequenos para que as contas sejam bem simples. Consideremos um motor de 60 RPM (quase um cata-vento). Logo, a polia motora tem 60rpm. A polia movida rodará a Xrpm. Não sabemos ainda, mas temos as informações fundamentais; os diâmetros. D1 tem 6mm e D2 tem 20mm. Agora, uma regra de 3 simples:

Me perdoem pela variação no tamanho das letras da fórmula, faz tempo que não mexo com o LyX e estou desabituado com Latex. Justificado isso, não vou representar mais com fórmula, vou direto para a conta.

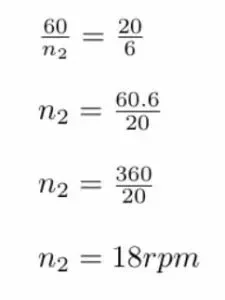
Agora, suponhamos que desejamos 18rpm e queremos descobrir o diâmetro ideal. Basta dividir o RPM motor pelo RPM pretendido e então multiplicar pelo diâmetro da polia maior, assim descobrimos o diâmetro da polia menor.:

18/60*20=6

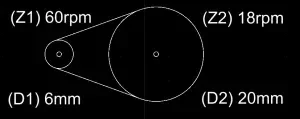
Podemos variar ambas as polias, considerando apenas a rotação do motor:

18/60*40=12

Ou ainda:

60*40/12=18

Agora vamos fazer só mais um cálculo.

D1 = 200

n1 = 60

n2 = 18

D2 = ?

18/60*200 = 60

Perceba que a polia pode variar de tamanho no motor, então calculamos a segunda polia. Mas a implicância disso está diretamente ligada à força. Por exemplo, um servo motor SG90 tem torque de 1.8kgf.cm. Em 3cm ele terá apenas 0.6kgf. Quanto maior for a polia no motor, menor será a força suportada na borda da roda. Para figurar, imagine esticar o braço segurando um pacote de 1kg de açúcar. Agora, Pegue uma vassoura, coloque o açúcar sobre a parte que varre o chão e erga novamente.Provavelmente você não conseguirá sequer erguer esse pacote de açúcar. Mais uma dica:

Quando for pensar em relação de força, pense no eixo do motor até a borda da engrenagem ou polia. Quanto maior a polia motora, maior será o esforço na borda. Agora a relação entre polias mais uma vez; quando uma polia menor gira uma polia maior, a velocidade é convertida em força para a segunda polia. Por isso é muito importante utilizar reduções. Vamos ver um conjunto de redução de 2 estágios.

Conjunto redutor de velocidade

Nesse artigo não estamos tratando de torque, veremos isso em outro artigo para não complicar o assunto. Ainda permaneceremos em cálculos reduzidos, como se estivéssemos usando um motor DC desses motores de carrinho à pilha.

Para esse exemplo, vamos usar o seguinte desenho:

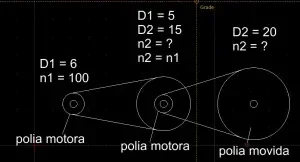
A simplicidade de calcular é a mesma. Primeiro, o conjunto das primeiras duas polias; motora e movida. Depois no segundo conjunto, a motora passa a ser a movida pela primeira polia. Isso é fácil de assimilar, a terceira só se move se a segunda se mover, logo, a segunda polia é motora da terceira.

n1 = 100 n2 = ? D2 = 15 D1 = 6 100/15*6 = 40rpm

Feito. Agora o segundo conjunto.

n1 = 40 n2 = ? d2 = 20 d1 = 5 40/20*5 = 10rpm

Fácil ou não?

Como calcular RPM de engrenagens

A fórmula (citada mais acima) difere no item Diâmetro (D), que será trocado por Dentes (Z). Vou usar como base as engrenagens do exemplo desse artigo.

Usando uma rotação bem baixa:

n1 = 20 n2 = ? Z2 = 20 Z1 = 10 2*10/20 = 10rpm

Ou seja, a menor é 50% do tamanho da maior, assim, ela roda 2 vezes para que a maior rode 1. Isso significa que a velocidade da maior é a metade da menor.

Em um trem de engrenagens o cálculo é o mesmo, seguindo a lógica do conjunto de polias. Veremos mais disso no artigo do relógio cuco que estou fazendo (não era pra falar, mas não resisti).

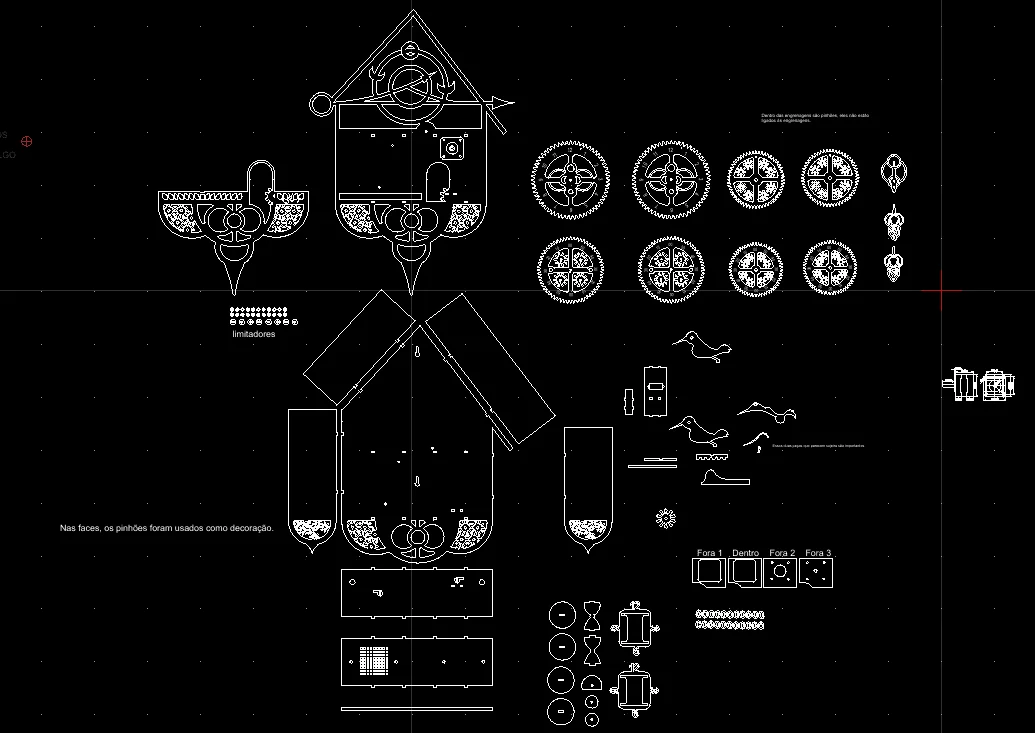
Da mesma forma que descobrimos o diâmetro da roda menor no exemplo mais acima, também podemos descobrir o número de dentes necessários para uma engrenagem apenas como exemplificado. O cálculo da engrenagem inicial dependerá da força pretendida ou, da redução dessa força. Por isso, não basta saber calcular redução, é necessário saber calcular torque também. Como os projetos que estamos fazendo não tem comprometimento industrial, não precisamos calcular resistência de materiais, mas se em algum momento o for, explico em um artigo.

Eu sei, teoria é chato, mas se você leu até essa linha, tenha certeza que esse artigo eu escrevi com carinho pra você e pra mim. Obrigado!

Inscreva-se no nosso canal Manual do Maker no YouTube.

Também estamos no Instagram.